On Generalizations of the Stirling Number Triangles ¹

Wolfdieter L a n g ²
Institut für Theoretische Physik
Universität Karlsruhe
Kaiserstraße 12, D-76128 Karlsruhe, Germany

Abstract:

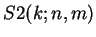
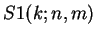
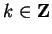
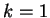
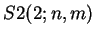
Sequences of generalized Stirling numbers of both kinds are presented. These sequences of triangles of numbers (or infinite dimensional lower triangular matrices) will be denoted by $S2(k;n,m)$ and $S1(k;n,m)$, with $k\in \bf Z$. The original Stirling number triangles of the second and first kind show up for $k=1$. 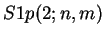$S2(2;n,m)$ is identical with the unsigned S1(2;n,m) triangle, called $S1p(2;n,m)$, which represents the triangle of signless Lah numbers. 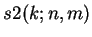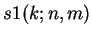Associated number triangles, called $s2(k;n,m)$ and $s1(k;n,m)$, are also defined. 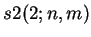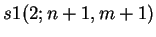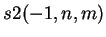$s2(2;n,m)$ as well as $s1(2;n+1,m+1)$ is Pascal's triangle, and $s2(-1,n,m)$ turns out to be Shapiro's Catalan triangle.

Generating functions for the columns of these triangles are given. Each 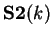${\bf S2}(k)$ and each 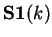${\bf S1}(k)$ matrix is an example of a Jabotinsky-matrix. Therefore, the generating functions of the rows of these triangular arrays constitute exponential convolution polynomials. The sequences of the row-sums of these triangles are also considered.

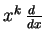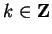The connection to the problem of finding finite transformations from infinitesimal ones generated by $x^k\,\frac {d{\ }}{dx\phantom{}}$, for $k\in \bf Z$, is made.