Riccati meets Fibonacci


Wolfdieter L a n g ¹

Institut für Theoretische Physik
Universität Karlsruhe
Kaiserstrasse 12, D-76128 Karlsruhe, Germany

Abstract:

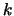
The generating functions for generalized Fibonacci and Lucas numbers are shown to be the unique solutions to Riccati equations with certain initial conditions. This observation leads directly to recursion relations for $k$-fold convolutions of these numbers which have been partly found earlier in a different way. A generalization of this method to so called 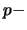$p-$Fibonacci numbers is also considered.

AMS MSC numbers: 11B83, 11B39, 11C08