Next: Convolutions of generalized Fibonacci
Up: p35
Previous: Introduction and Summary
Lemma 1:  defined in eq. 2 satisfies eq. 13.
defined in eq. 2 satisfies eq. 13.
Proof: This follows from the identity
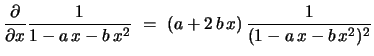 |
(58) |
after multiplication with
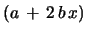 and separation of the last term
in eq. 13.
and separation of the last term
in eq. 13. .
.
Corollary 1: For the non-degenerate case
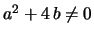 this is a
Riccati eq. (also a special Bernoulli eq.) which can be written
as shown in eq. 15.
this is a
Riccati eq. (also a special Bernoulli eq.) which can be written
as shown in eq. 15.
In the degenerate case
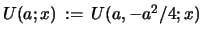 satisfies the first
order linear differential eq. 27 as well as the second order
non-linear differential eq. given as the first of eqs. 29.
satisfies the first
order linear differential eq. 27 as well as the second order
non-linear differential eq. given as the first of eqs. 29.
Proof: Elementary. 
Note 1: The degenerate case is equivalent to
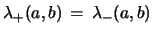 with the definition of the characteristic roots of
the recursion relation eq. 1 given in eq. 4. We may
assume that not both,
with the definition of the characteristic roots of
the recursion relation eq. 1 given in eq. 4. We may
assume that not both, 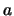 and
and 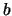 , vanish and
, vanish and
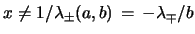 . In each case
. In each case
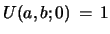 .
.
Lemma 2: 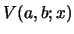 defined in eq. 3 for
defined in eq. 3 for 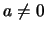 satisfies
eq. 14.
satisfies
eq. 14.
Proof: This follows from the identity
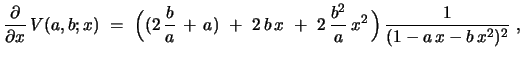 |
(59) |
after multiplication with
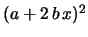 and separation of the
and separation of the
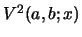 term shown in eq. 14.
term shown in eq. 14.
Corollary 2: For the non-degenerate case
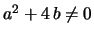 eq. 14 is a Riccati eq. which can be written as shown in
eq. 16.
eq. 14 is a Riccati eq. which can be written as shown in
eq. 16.
In the degenerate case
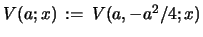 satisfies the first
order linear differential eq. 28 as well as the first order
non-linear differential eq. given as the second of eqs. 29.
satisfies the first
order linear differential eq. 28 as well as the first order
non-linear differential eq. given as the second of eqs. 29.
In each case
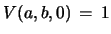 .
.
Proof: Elementary. 
Proposition 1 (Solution of eq. 13):
a) For
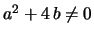 the solution of the Riccati eq. 13
with
the solution of the Riccati eq. 13
with
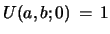 is given by eq. 2.
is given by eq. 2.
b) For
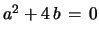 the solution of eqs. 27 is
the solution of eqs. 27 is
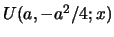 from eq. 2.
from eq. 2.
Proof: a) Rewrite this Riccati eq., which is also of the Bernoulli type,
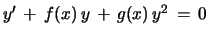 with
with
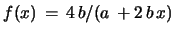 and
and
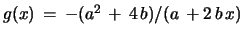 , provided
, provided
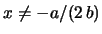 , as a
first order inhomogeneous linear differential eq. for
, as a
first order inhomogeneous linear differential eq. for 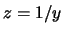 :
:
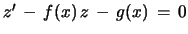 . Its standard solution is
. Its standard solution is
![$ y^{-1}\, =\, z\, =\,
exp(F(x))\, \left[ C\, +\, \int\, dx\,exp(F(x))\, g(x)\right] $](img247.gif) with
with
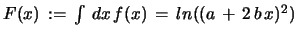 . The integral becomes
. The integral becomes
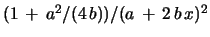 and
and 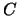 is fixed from the initial
value
is fixed from the initial
value
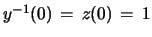 to
to 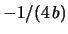 . The solution
. The solution
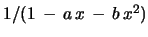 is also correct if
is also correct if
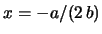 .
.
b) For
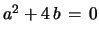 and
and 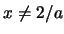 the solution of the standard linear differential eq. 27 coincides with eq. 2.
For
the solution of the standard linear differential eq. 27 coincides with eq. 2.
For
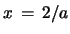 eq. 27 demands a singular
eq. 27 demands a singular
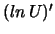 ; a requirement which is satisfied by this solution.
; a requirement which is satisfied by this solution. 
Proposition 2 (Solution of eq. 14):
a) For
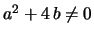 the solution of the Riccati eq. 14
with
the solution of the Riccati eq. 14
with 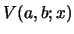 is given by eq. 3.
is given by eq. 3.
b) For
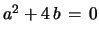 the solution of eqs. 28 is
the solution of eqs. 28 is
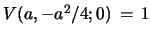 from eq. 3.
from eq. 3.
Proof: a) Similar to the proof of Proposition 1 as standard
solution to the inhomogeneous linear differential eq. for
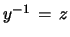 where now
where now
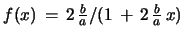 ,
,
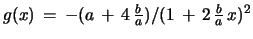 and
and
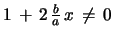 . The initial value is
. The initial value is
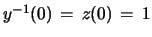 which fixes the solution to be
which fixes the solution to be
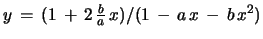 . This is also correct for
. This is also correct for
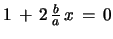 .
.
b) For
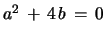 and
and 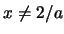 the solution of eq. 28 with
the solution of eq. 28 with
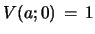 coincides with
coincides with
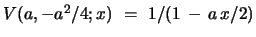 . For
. For
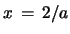 eq. 28 needs a singular
eq. 28 needs a singular
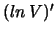 because
because 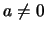 , and this requirement is indeed fulfilled.
, and this requirement is indeed fulfilled. 



Next: Convolutions of generalized Fibonacci
Up: p35
Previous: Introduction and Summary
Wolfdieter Lang
2002-04-04