


Next: Riccati equations for Fibonacci
Up: p35
Previous: p35
The generating function for generalized Fibonacci numbers
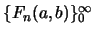 , defined by the three term recurrence relation
, defined by the three term recurrence relation
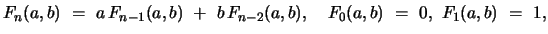 |
(1) |
with given real 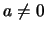 and
and 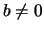 , is well-known. For arbitrary
, is well-known. For arbitrary
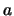 and
and 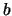 ,
,
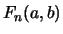 can be considered as a polynomial in two variables.
If one considers the numbers, or polynomials,
can be considered as a polynomial in two variables.
If one considers the numbers, or polynomials,
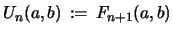 one
has from the recursion with input
one
has from the recursion with input
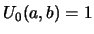 and
and
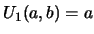 (or
(or
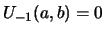 )
)
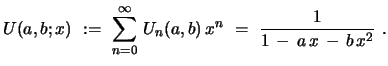 |
(2) |
Similarly, for the generalized Lucas numbers
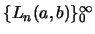 which satisfy the same recursion
eq. 1 but with inputs
which satisfy the same recursion
eq. 1 but with inputs
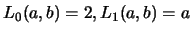 , one finds, with
, one finds, with
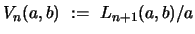 , remembering that
, remembering that 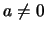 ,
,
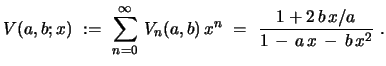 |
(3) |
The input is now
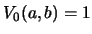 and
and
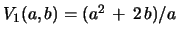 (or
(or
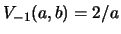 ).
).
These (ordinary) generating functions can also be written in terms of the
characteristic roots corresponding to the recursion relation
eq. 1
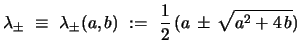 |
(4) |
as follows.
The corresponding Binet forms of the corresponding numbers are in the non-degenerate
case
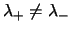 , i.e.
, i.e.
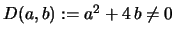 ,
,
In the degenerate case one has
The explicit form of these polynomials is
This result for
 follows from a combinatorial interpretation of the
recurrence relation, and the one for
follows from a combinatorial interpretation of the
recurrence relation, and the one for
 is due to the Girard
-Waring formula in its simplest version (for this cf. [4],
[3], also for original refs.).
is due to the Girard
-Waring formula in its simplest version (for this cf. [4],
[3], also for original refs.).
The observation reported in this work is that the generating functions eq. 2 (or eq. 5) and eq. 3 (or eq. 6) are the unique solutions to the following special type of Riccati eqs. (simultaneously a special type of Bernoulli eq. For the
history of such eqs. see [9], ch.I, 1.1)
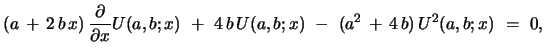 |
(13) |
with the initial condition
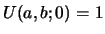 . Similarly,
. Similarly,
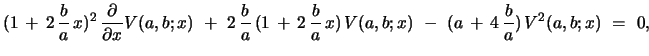 |
(14) |
with the initial condition
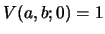 . Such Riccati eqs. can be
transformed to inhomogeneous linear differential eqs. of first order. Our
interest here is to use these eqs. in order to obtain information about
. Such Riccati eqs. can be
transformed to inhomogeneous linear differential eqs. of first order. Our
interest here is to use these eqs. in order to obtain information about
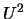 and
and 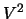 .
The degenerate case
.
The degenerate case
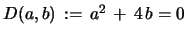 , for which the above
given differential eqs. become linear, will be considered separately.
, for which the above
given differential eqs. become linear, will be considered separately.
These Riccati eqs. immediately allow one to express convolutions of
Fibonacci or Lucas sequences in terms of these numbers. In the
non-degenerate case,
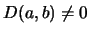 , one rewrites the Riccati
eqs. as
, one rewrites the Riccati
eqs. as
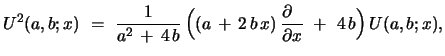 |
(15) |
and
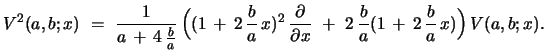 |
(16) |
The (first) convolution of these sequences, which we call
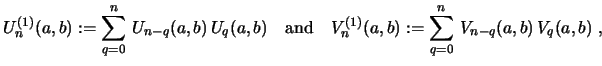 |
(17) |
and whose generating functions are
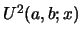 and
and
 , respectively, satisfy therefore
, respectively, satisfy therefore
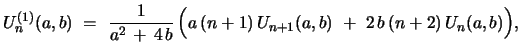 |
(18) |
and
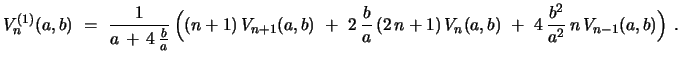 |
(19) |
After use of the recursion relation eq. 1 the last eq. can be
written in the form
![$\displaystyle V^{(1)}_{n}(a,b)\ =\ {\frac{1}{a\,(a^2 \, +\, 4\,b)}}\,\Bigl{(}\b...
...n+1) \,\ +\ 4\,b\,n\bigr{]}\, V_{n+1}(a,b)\ +\ 2\, b\, a\,V_{n}(a,b)\Bigr{)}\ .$](img59.gif) |
(20) |
For 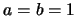 one recovers well-known formulae for convolutions of ordinary
Fibonacci, resp. Lucas numbers (e.g. [7], p.183, eqs. (98) and (99) (with corrected
one recovers well-known formulae for convolutions of ordinary
Fibonacci, resp. Lucas numbers (e.g. [7], p.183, eqs. (98) and (99) (with corrected
 )). To see this, observe
that
)). To see this, observe
that
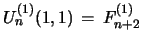 and
and
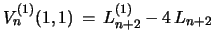 .
.
For the  th convolution
th convolution
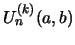 and
and
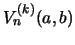 , with
, with
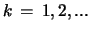 , one employs in the case
, one employs in the case
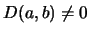 the following identities which
follow from the Riccati eqs.
the following identities which
follow from the Riccati eqs.
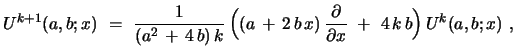 |
(23) |
and
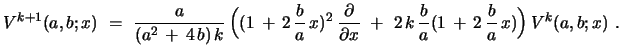 |
(24) |
These identities allow one to express the  th convolution, generated
by
th convolution, generated
by
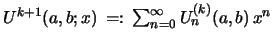 , in terms of the
, in terms of the 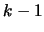 -st one according to
-st one according to
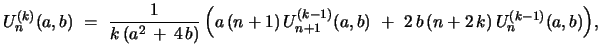 |
(25) |
with input
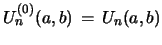 , and
, and
with input
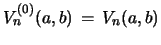 .
The formula given in eq. 25 has been found earlier in
[1] (p. 202, III and p.213, eq. (30)) without using the
defining Riccati eq. for
.
The formula given in eq. 25 has been found earlier in
[1] (p. 202, III and p.213, eq. (30)) without using the
defining Riccati eq. for  . The notations have to be
translated with the help of
. The notations have to be
translated with the help of
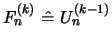 ,
,
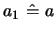 ,
and
,
and
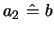 .
.
Before discussing iteration of these recursion relations we state the results
for the degenerate case
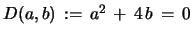 . The Riccati eqs. 13 and 14
collapse to linear differential eqs. for
. The Riccati eqs. 13 and 14
collapse to linear differential eqs. for
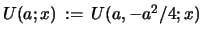 and
and
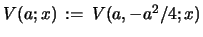
For the last eq. 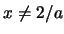 was assumed. Because the solutions to these
eqs. imply
was assumed. Because the solutions to these
eqs. imply
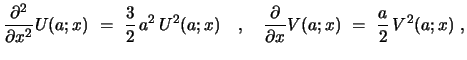 |
(29) |
the corresponding first (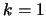 ) convolutions of these numbers
) convolutions of these numbers
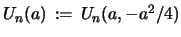 and
and
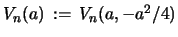 are given by
are given by
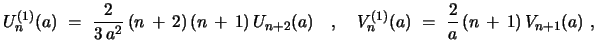 |
(30) |
with eqs. 9 and 10.
In order to derive the result for the  th convolution one starts with
identities which follow from the solutions of eqs. 27 and 28, namely
th convolution one starts with
identities which follow from the solutions of eqs. 27 and 28, namely
These identities imply for the  th convolutions
th convolutions
with inputs
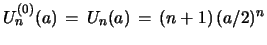 and
and
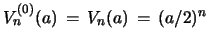 . See eqs. 9 and
10.
. See eqs. 9 and
10.
The iteration of these eqs. yields the final result, which for 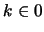 ,
and in the degenerate case
,
and in the degenerate case
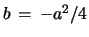 , is
, is
Thus
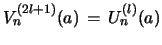 , and it suffices to treat
, and it suffices to treat
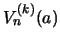 . For even
. For even 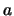 these are
non-negative integer sequences. For
these are
non-negative integer sequences. For
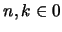 ,
,
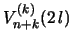 constitutes a convolution triangle of numbers based on the
constitutes a convolution triangle of numbers based on the 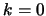 column sequence
column sequence
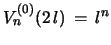 (powers of
(powers of 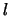 ). See [5] for these triangles of numbers.
). See [5] for these triangles of numbers.
In the non-degenerate case the recursion relation eq. 24 can be
iterated in order to express the  th convolution of
th convolution of
 as linear
combination of these numbers according to
as linear
combination of these numbers according to
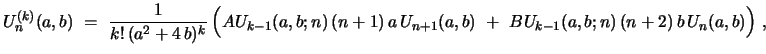 |
(37) |
with certain polynomials
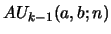 and
and
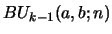 of degree
of degree
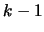 in the variable
in the variable 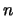 , for arbitrary, but fixed,
, for arbitrary, but fixed, 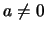 ,
, 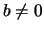 , and
, and
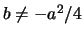 .
.
The (mixed) recursion relations for these polynomials are deduced from
eq. 24, and for
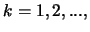 they are
they are
with inputs
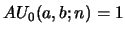 and
and
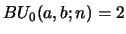 .
.
In eqs. (26), resp. (27), of [1] one can find explicit results for
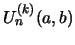 for the instances
for the instances 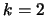 , resp.
, resp. 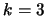 (in eq. (26) of this
ref. one has to multiply the lhs with
(in eq. (26) of this
ref. one has to multiply the lhs with 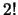 , and in the second line of
, and in the second line of
 of eq.
of eq.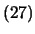 it should read
it should read 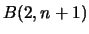 ).
).
For the case 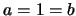 the triangles of the coefficients of these
polynomials can be viewed under the nrs. A057995 and A057280 in [5].
For
the triangles of the coefficients of these
polynomials can be viewed under the nrs. A057995 and A057280 in [5].
For
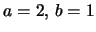 see A058402 and A058403.
see A058402 and A058403.
Similarly, iteration of recursion eq. 25 results, with the help of
the recursion relation eq. 1, in
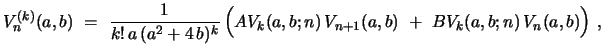 |
(40) |
with certain polynomials
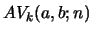 and
and
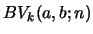 of generic
degree
of generic
degree 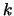 in the variable
in the variable 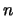 , for fixed
, for fixed 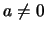 ,
, 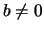 , with
, with
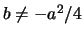 .
.
The (mixed) recursion relations for these polynomials are found from
eq. 26, and for 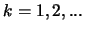 , they are
, they are
with inputs
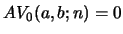 and
and
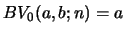 .
.
For 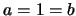 the triangles of coefficients of these polynomials in
the triangles of coefficients of these polynomials in 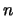 can be found under the nrs. A061188 and A061189 in [5]. Observe that
can be found under the nrs. A061188 and A061189 in [5]. Observe that
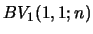 is accidentally of degree 0. For
is accidentally of degree 0. For 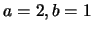 see nrs.
A062133 and A062134. For
see nrs.
A062133 and A062134. For
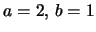 see A062133 and A062134.
see A062133 and A062134.
Motivated by a recent paper [6] we consider also the following
generalized 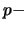 Fibonacci numbers
Fibonacci numbers
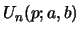 defined for
defined for 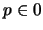 by the generating function
by the generating function
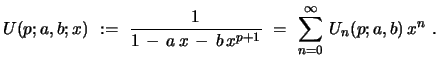 |
(43) |
Of course, we assume 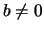 and also take
and also take 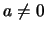 . For
. For 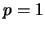 these numbers reduce to the
these numbers reduce to the
 treated above, and for
treated above, and for 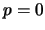 they become the powers
they become the powers 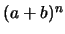 .
.
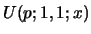 appears in eq. 71 of [2]. The recursion relations
are
appears in eq. 71 of [2]. The recursion relations
are
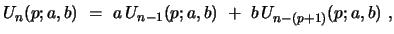 |
(44) |
with inputs
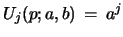 for
for
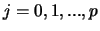 .
In order to derive expressions for the
.
In order to derive expressions for the  th convolution of these
th convolution of these
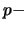 Fibonacci numbers consider first the following Riccati eq.
satisfied by
Fibonacci numbers consider first the following Riccati eq.
satisfied by
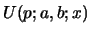 written for the non-degenerate case
written for the non-degenerate case
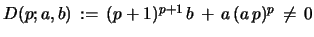 if
if
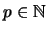 , and
, and
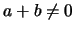 if
if 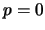 (i.e. one puts
(i.e. one puts
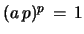 if
if 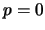 ).
).
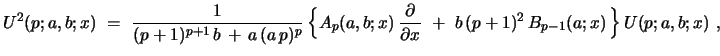 |
(45) |
with
For 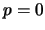 one has to use
one has to use
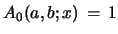 and
and
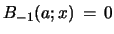 .
For given non-vanishing
.
For given non-vanishing 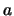 and
and 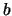 these polynomials
these polynomials
 , resp.
, resp.
 , in the variable
, in the variable 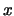 of degree
of degree 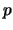 , resp.
, resp. 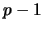 ,
have therefore the following explicit form.
,
have therefore the following explicit form.
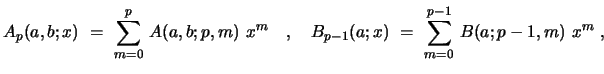 |
(48) |
with the coefficients
For
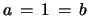 these triangles of coefficients can be viewed under the numbers
these triangles of coefficients can be viewed under the numbers 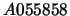 and
and 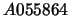 in [5] where further details may
be found.
in [5] where further details may
be found.
Even though we cannot integrate the linear differential eq., which is equivalent to the Riccati eq. 45 for
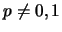 , analytically, the above given solution is its unique one due to
the existence and uniqueness theorem for the linear first order differential
eq. satisfied by
, analytically, the above given solution is its unique one due to
the existence and uniqueness theorem for the linear first order differential
eq. satisfied by
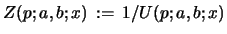 with initial value
with initial value
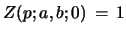 .
.
The result for the first (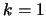 ) convolution of the numbers
) convolution of the numbers
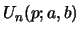 which flows from the Riccati eq. is
which flows from the Riccati eq. is
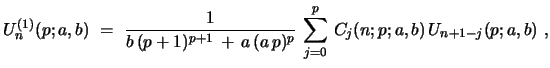 |
(51) |
with
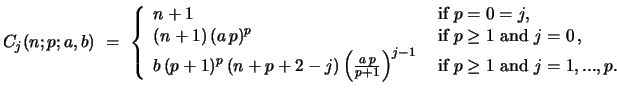 |
(52) |
The
 recursion cannot be used to simplify the sum
in eq. 51.
recursion cannot be used to simplify the sum
in eq. 51.
This result can now be compared, after putting  , with a
different formula for the same convolution found in [6],
eq.(14). For given
, with a
different formula for the same convolution found in [6],
eq.(14). For given  and
and
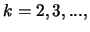 the
recursion for
the
recursion for
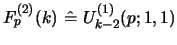 in
[6] involves all
in
[6] involves all 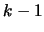 terms
terms
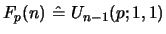 ,
for
,
for
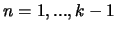 , whereas our result needs only
, whereas our result needs only 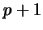 terms for all
terms for all 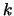 .
For example,
.
For example,
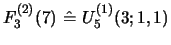 is reduced to six
terms involving
is reduced to six
terms involving
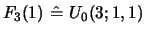 ,...,
,...,
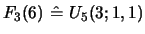 in [6], but only to four terms,
involving
in [6], but only to four terms,
involving
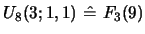 ,
,
 ,...,
,...,
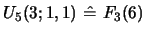 in eq. 51.
in eq. 51.
For the  th convolution one uses the following identity which derives from
the Riccati eq. 45. It is written for the non-degenerate case,
and is valid for
th convolution one uses the following identity which derives from
the Riccati eq. 45. It is written for the non-degenerate case,
and is valid for
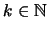 .
.
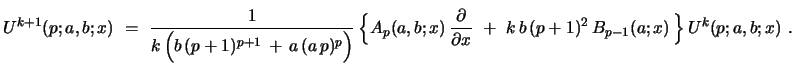 |
(53) |
For 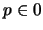 the corresponding recursion relation for the
the corresponding recursion relation for the
 th convolution is (remember that one puts
th convolution is (remember that one puts
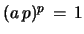 if
if 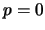 )
)
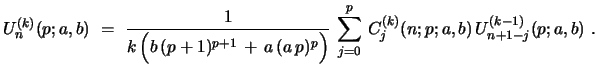 |
(54) |
with
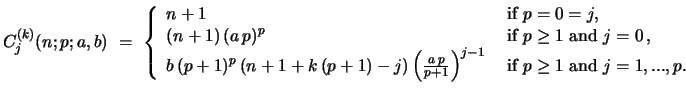 |
(55) |
Instead of showing the rather unwieldy formula for this iterated recursion
relation after employing the fundamental recursion eq. 1 we
prefer to state the result for the instance
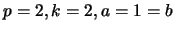 , with the
notation
, with the
notation
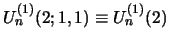 and
and
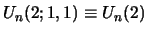 :
:
The recursion relation eq. 1 has been used twice.
In the degenerate case
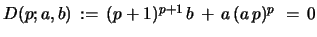 (where one puts
(where one puts
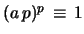 if
if 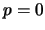 ) one finds for
) one finds for
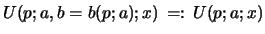 , where
, where
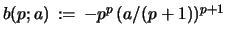 , the linear differential eq.
, the linear differential eq.
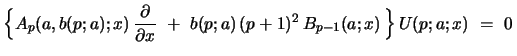 |
(57) |
with 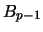 and
and 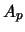 taken in their explicit form known from
eqs. 47 and 46. For general
taken in their explicit form known from
eqs. 47 and 46. For general 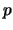 and
and
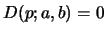 we
cannot say anything about convolution because we have no suitable expression
for
we
cannot say anything about convolution because we have no suitable expression
for
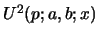 .
The recurrence eq. 1 with depth
.
The recurrence eq. 1 with depth 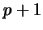 can be replaced by one with
only depth
can be replaced by one with
only depth 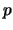 . See eq. 73.
. See eq. 73.
In the non-degenerate case one could also consider the other 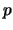 linear
independent (Lucas-type) sequences defined by the recurrence
eq. and appropriate inputs but we will not do this here.
linear
independent (Lucas-type) sequences defined by the recurrence
eq. and appropriate inputs but we will not do this here.
The remainder of this paper provides proofs for the above given statements.



Next: Riccati equations for Fibonacci
Up: p35
Previous: p35
Wolfdieter Lang
2002-04-04
![]() , one rewrites the Riccati
eqs. as
, one rewrites the Riccati
eqs. as
![]() . The Riccati eqs. 13 and 14
collapse to linear differential eqs. for
. The Riccati eqs. 13 and 14
collapse to linear differential eqs. for
![]() and
and
![]()
![]() are given by
are given by
![]() ,
and in the degenerate case
,
and in the degenerate case
![]() , is
, is
![]() they are
they are
![]() for the instances
for the instances ![]() , resp.
, resp. ![]() (in eq. (26) of this
ref. one has to multiply the lhs with
(in eq. (26) of this
ref. one has to multiply the lhs with ![]() , and in the second line of
, and in the second line of
![]() of eq.
of eq.![]() it should read
it should read ![]() ).
).
![]() the triangles of the coefficients of these
polynomials can be viewed under the nrs. A057995 and A057280 in [5].
For
the triangles of the coefficients of these
polynomials can be viewed under the nrs. A057995 and A057280 in [5].
For
![]() see A058402 and A058403.
see A058402 and A058403.
![]() , they are
, they are
![]() the triangles of coefficients of these polynomials in
the triangles of coefficients of these polynomials in ![]() can be found under the nrs. A061188 and A061189 in [5]. Observe that
can be found under the nrs. A061188 and A061189 in [5]. Observe that
![]() is accidentally of degree 0. For
is accidentally of degree 0. For ![]() see nrs.
A062133 and A062134. For
see nrs.
A062133 and A062134. For
![]() see A062133 and A062134.
see A062133 and A062134.
![]() , analytically, the above given solution is its unique one due to
the existence and uniqueness theorem for the linear first order differential
eq. satisfied by
, analytically, the above given solution is its unique one due to
the existence and uniqueness theorem for the linear first order differential
eq. satisfied by
![]() with initial value
with initial value
![]() .
.
![]() ) convolution of the numbers
) convolution of the numbers
![]() which flows from the Riccati eq. is
which flows from the Riccati eq. is
![]() , with a
different formula for the same convolution found in [6],
eq.(14). For given
, with a
different formula for the same convolution found in [6],
eq.(14). For given ![]() and
and
![]() the
recursion for
the
recursion for
![]() in
[6] involves all
in
[6] involves all ![]() terms
terms
![]() ,
for
,
for
![]() , whereas our result needs only
, whereas our result needs only ![]() terms for all
terms for all ![]() .
For example,
.
For example,
![]() is reduced to six
terms involving
is reduced to six
terms involving
![]() ,...,
,...,
![]() in [6], but only to four terms,
involving
in [6], but only to four terms,
involving
![]() ,
,
![]() ,...,
,...,
![]() in eq. 51.
in eq. 51.
![]() th convolution one uses the following identity which derives from
the Riccati eq. 45. It is written for the non-degenerate case,
and is valid for
th convolution one uses the following identity which derives from
the Riccati eq. 45. It is written for the non-degenerate case,
and is valid for
![]() .
.