


Next: Convolutions of generalized Fibonacci
Up: p35
Previous: Riccati equations for Fibonacci
The Riccati eqs. 13, resp. 14, are replaced in the
non-degenerate case by eqs. 15, resp. 16. Because the
 th power of the (ordinary) generating functions of a sequence
generates
th power of the (ordinary) generating functions of a sequence
generates  fold convolutions of this sequence one obtains the expression
eq. 18, resp. eq. 19. For the definition of the first
convolutions
fold convolutions of this sequence one obtains the expression
eq. 18, resp. eq. 19. For the definition of the first
convolutions
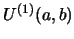 and
and
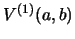 see eqs. 17.
Eq. 19 simplifies to eq. 20 after use of the recurrence
relation eq. 1. In this way the first
convolutions can be determined in each case from linear combinations of the two independent
original sequences. For
see eqs. 17.
Eq. 19 simplifies to eq. 20 after use of the recurrence
relation eq. 1. In this way the first
convolutions can be determined in each case from linear combinations of the two independent
original sequences. For
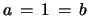 these formulae
are well-known (see the Introduction after eq. 20). The
generalization to arbitrary
these formulae
are well-known (see the Introduction after eq. 20). The
generalization to arbitrary
 fold convolutions is now straightforward.
fold convolutions is now straightforward.
Lemma 3 (Recurrencce for  fold convolutions):
fold convolutions):
In the non-degenerate case
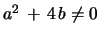 the recurrence eq. 25, resp. eq. 26, holds for the
the recurrence eq. 25, resp. eq. 26, holds for the  fold convolution of generalized Fibonacci, resp. Lucas, sequences.
fold convolution of generalized Fibonacci, resp. Lucas, sequences.
Proof: This is a direct consequence of the identities for the 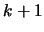 st
power of
st
power of  , resp.
, resp. 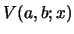 shown in eq. 23, resp. eq. 24. These identities, in turn, result after induction over
shown in eq. 23, resp. eq. 24. These identities, in turn, result after induction over 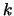 with the
basis
with the
basis 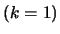 provided by eq. 15, resp. eq. 16.
Because of
provided by eq. 15, resp. eq. 16.
Because of
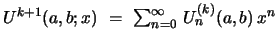 , and the same eq. with
, and the same eq. with 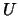 replaced by
replaced by 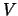 , one arrives at eq. 25, resp. eq. 26.
, one arrives at eq. 25, resp. eq. 26.
Lemma 4 (Recurrence for  fold convolution, degenerate case):
fold convolution, degenerate case):
For
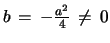 the recurrence formulae for the
the recurrence formulae for the  fold convolution of the generalzed Fibonacci, resp. Lucas,
sequences are those stated in eqs. 33, resp. 34.
fold convolution of the generalzed Fibonacci, resp. Lucas,
sequences are those stated in eqs. 33, resp. 34.
Proof: This statement is equivalent to eq. 31, resp.
eq. 32 for the powers of the corresponding generating functions.
They are deduced from the the second, resp. first, order differential eq.
given in eq. 29 which is identical with the 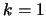 assertion. To
verify the general
assertion. To
verify the general  claim eq. 31, resp. eq. 32, one may
use
claim eq. 31, resp. eq. 32, one may
use
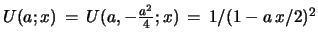 from
eq. 2, resp.
from
eq. 2, resp.
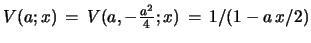 from eq. 3.
from eq. 3.
Lemma 5: The explicit form for the  fold convolution in the
degenerate case is given by eq. 35, resp. 36, for the
generalized Fibonacci, resp. Lucas, case.
fold convolution in the
degenerate case is given by eq. 35, resp. 36, for the
generalized Fibonacci, resp. Lucas, case.
Proof: Iteration of the recurrence eq. 33, resp.
eq. 34, with input
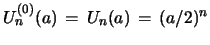 , resp.
, resp.
 , which originates from the
generating functions
, which originates from the
generating functions
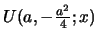 , resp.
, resp.
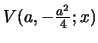 .
. 
Proposition 3 (Iteration of recurrence for  fold convolutions; non-degenerate Fibonacci case):
fold convolutions; non-degenerate Fibonacci case):
For
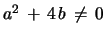 the
the  fold convolution of the generalized
Fibonacci sequence
fold convolution of the generalized
Fibonacci sequence
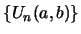 is expressed as linear combinations of the two independent solutions of recurrence eq. 1 as given in
eq. 37. The coefficient polynomials
is expressed as linear combinations of the two independent solutions of recurrence eq. 1 as given in
eq. 37. The coefficient polynomials
 and
and
 satisfy the mixed recurrence relations eqs. 38 and
39.
satisfy the mixed recurrence relations eqs. 38 and
39.
Proof: If one considers eq. 37 as ansatz and puts it into the recurrence eq. 25 one finds, after elimination of
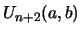 via its recursion relation and a comparison of the coefficients of the linear independent
via its recursion relation and a comparison of the coefficients of the linear independent
 and
and
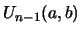 sequences, the mixed recurrence relations for
sequences, the mixed recurrence relations for
 and
and
 . The inputs
. The inputs
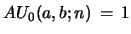 and
and
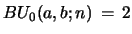 are necessary in order
that for
are necessary in order
that for 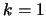 eq. 37 coincides with eq. 18. With these
inputs and the mixed recurrence one proves, by induction over
eq. 37 coincides with eq. 18. With these
inputs and the mixed recurrence one proves, by induction over 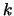 , that
, that
 and
and
 are polynomials in
are polynomials in 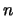 of degree
of degree 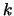 , provided
, provided 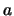 and
and 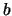 are fixed with
are fixed with
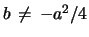 ,
,
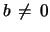 and
and
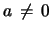 .
.

Note 2: For integers 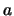 and
and
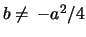 the coefficients of
the polynomials
the coefficients of
the polynomials
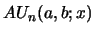 and
and
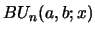 furnish two lower
triangular integer matrices. For the ordinary Fibonacci case
furnish two lower
triangular integer matrices. For the ordinary Fibonacci case  these positive integer triangles can be found in [5] under the nrs.
A057995 and A057280. For the Pell case
these positive integer triangles can be found in [5] under the nrs.
A057995 and A057280. For the Pell case
 see nrs. A058402 and A058403.
see nrs. A058402 and A058403.
Proposition 4 (Iteration of recurrence for  fold convolutions; non-degenerate Lucas case):
fold convolutions; non-degenerate Lucas case):
For
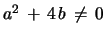 the
the  fold convolution of the generalized
Lucas sequence
fold convolution of the generalized
Lucas sequence
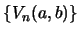 is expressed as linear combination
of the two independent solutions of recurrence eq. 1 as given in
eq. 40. The coefficient polynomials
is expressed as linear combination
of the two independent solutions of recurrence eq. 1 as given in
eq. 40. The coefficient polynomials
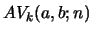 and
and
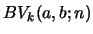 satisfy the mixed recurrence relations eq. 41 and
eq. 42.
satisfy the mixed recurrence relations eq. 41 and
eq. 42.
Proof: Analogous to the one of Proposition 3. 
Note 3: For integers 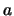 and
and
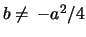 the coefficients of
the polynomials
the coefficients of
the polynomials
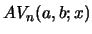 and
and
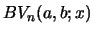 furnish two lower
triangular integer matrices. For the ordinary Lucas case
furnish two lower
triangular integer matrices. For the ordinary Lucas case 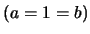 these positive integer triangles can be found in [5] under the nrs.
A061188 and A061189. For the Pell case
these positive integer triangles can be found in [5] under the nrs.
A061188 and A061189. For the Pell case
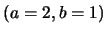 see nrs. A062133
and A062134.
see nrs. A062133
and A062134.



Next: Convolutions of generalized Fibonacci
Up: p35
Previous: Riccati equations for Fibonacci
Wolfdieter Lang
2002-04-04