


Next: Acknowledgements
Up: p35
Previous: Convolutions of generalized Fibonacci
Generalized 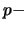 Fibonacci numbers
Fibonacci numbers
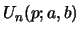 are defined by
eq. 1 for
are defined by
eq. 1 for 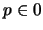 ,
, 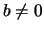 and
and 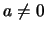 , together with the
inputs
, together with the
inputs
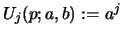 for
for 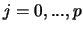 . For
. For 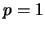 one recovers the generalized Fibonacci numbers
one recovers the generalized Fibonacci numbers
 treated above.
treated above.
Lemma 6: The generating function
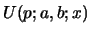 for the generalized
for the generalized
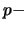 Fibonacci numbers is given by eq. 43.
Fibonacci numbers is given by eq. 43.
Proof: From the recurrence with inputs given in eq. 1.

Lemma 7 (Riccati eq. for the generalized 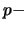 Fibonacci case):
Fibonacci case):
If
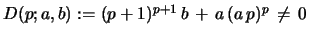 (non-degenerate
case) then
(non-degenerate
case) then
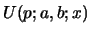 satisfies the Riccati eq. 45 with the
polynomials
satisfies the Riccati eq. 45 with the
polynomials
 and
and
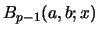 defined in
eqs. 46 and 47.
defined in
eqs. 46 and 47.
Proof: Use the ansatz
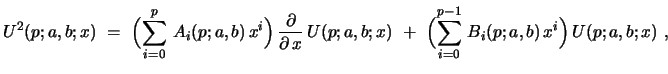 |
(60) |
together with
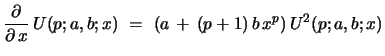 |
(61) |
from eq. 43. This implies
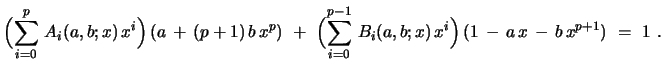 |
(62) |
Comparing first coefficients of the powers 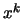 , for
, for
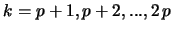 ,
leads to the eqs. (remember that
,
leads to the eqs. (remember that 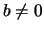 )
)
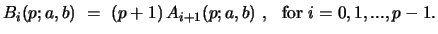 |
(63) |
With this result the coefficients of the powers 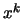 for
for
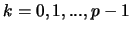 become, after iteration,
become, after iteration,
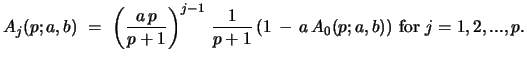 |
(64) |
Therefore the eqs. 63 are now
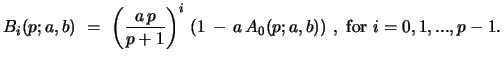 |
(65) |
Finally, the coefficient of 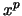 has to satisfy
has to satisfy
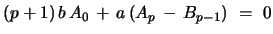 which implies, together with the above results,
which implies, together with the above results,
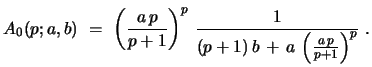 |
(66) |
Inserting this into the above found expressions finally leads to
With
one thus finds eqs. 47 and 46. The assertion can now be
proved directly with the found polynomials. 
Note 4: i) If 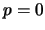 ,
,
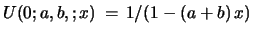 generates
powers of
generates
powers of 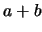 , and one has to put
, and one has to put
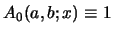 and
and
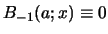 . This means that one puts
. This means that one puts
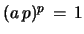 for
for 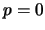 .
.
ii) For given non-vanishing 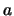 and
and 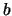
 is a polynomial in
is a polynomial in 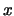 of
degree
of
degree 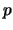 , and
, and
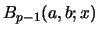 is one of degree
is one of degree 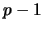 . The sum in
. The sum in
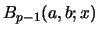 can be evaluated to yield the second of eqs. 47
provided
can be evaluated to yield the second of eqs. 47
provided 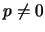 .
.
Lemma 8 (Coefficient triangles of numbers for polynomials
 and
and
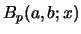 ):
):
The coefficients of the polynomials defined in eqs. 48 are given
by eqs. 49 and 50.
Proof:
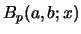 from eq. 47 leads immediately to
eq. 50, remembering that
from eq. 47 leads immediately to
eq. 50, remembering that
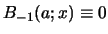 . Then eq. 49
follows from eq. 46 and
. Then eq. 49
follows from eq. 46 and
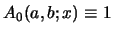 .
. 
Proposition 5 (Uniqueness of Riccati solution; non-degenerate
case):
If
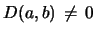 then
then
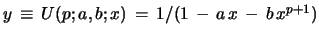 is the unique solution of the
Riccati eq. 45 with eqs. 46, 47 and
initial value
is the unique solution of the
Riccati eq. 45 with eqs. 46, 47 and
initial value
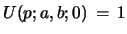 .
.
Proof: As a special Bernoulli eq. the Riccati eq.
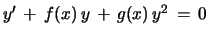 is equivalent to the inhomogeneous linear differential eq. for
is equivalent to the inhomogeneous linear differential eq. for
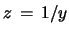 :
:
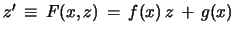 . Because
. Because 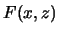 is continuous in the strip
is continuous in the strip
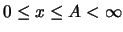 ,
,
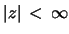 and is there
and is there
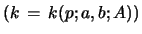 -Lipschitz,
the existence and uniqueness theorem for linear differential eqs. proves the
assertion (see e.g.[8], §6,I, p.62ff). In order to find
-Lipschitz,
the existence and uniqueness theorem for linear differential eqs. proves the
assertion (see e.g.[8], §6,I, p.62ff). In order to find 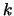 one uses the summed expression for
one uses the summed expression for 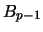 from eq. 47 and repeated
applications of the triangle inequality.
from eq. 47 and repeated
applications of the triangle inequality.
Lemma 9 (First convolution of
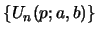 ; non-degenerate case):
; non-degenerate case):
The first convolution of the sequence
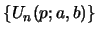 , which is defined
analogously to the first of eqs. 17, is given by eq. 51
with eq. 52.
, which is defined
analogously to the first of eqs. 17, is given by eq. 51
with eq. 52.
Proof: One has to compute the coefficients of 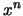 of the lhs of
eq. 45, taking into account the
of the lhs of
eq. 45, taking into account the 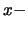 dependence of
dependence of 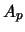 and
and
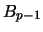 with the coefficients from eqs. 49 and 50.
The case
with the coefficients from eqs. 49 and 50.
The case 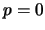 has to be considered separately. The recurrence eq. 1
cannot be used in order to simplify the sum in eq. 51.
has to be considered separately. The recurrence eq. 1
cannot be used in order to simplify the sum in eq. 51. 
Proposition 6 (Recurrence for 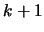 st power of the generating function
st power of the generating function
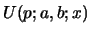 ; non-degenerate case):
; non-degenerate case):
For
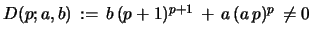 eq. 53 gives
eq. 53 gives
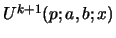 .
.
Proof:
due to eq. 45.
Proposition 7 ( fold convolution of
fold convolution of
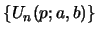 ; non-degenerate case):
; non-degenerate case):
For
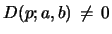 the entry
the entry
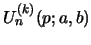 of the
of the  fold convolution of the sequence
fold convolution of the sequence
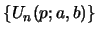 is given by eq. 54.
is given by eq. 54.
Proof: This follows immediately from Proposition 5 after comparing
coefficients of  using the definition
using the definition
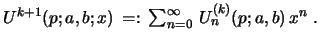

Lemma 10 (Degenerate case
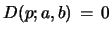 ):
):
If
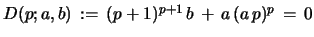 then
then
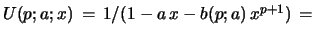
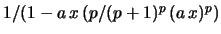 satisfies the first order linear differential eq. 57.
satisfies the first order linear differential eq. 57.
Proof: One proves
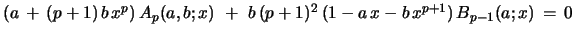 with eqs. 47 and 46 in the version where the sum has been evaluated (the case
with eqs. 47 and 46 in the version where the sum has been evaluated (the case 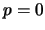 is
treated separately). If one factors out
is
treated separately). If one factors out
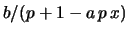 one finds that all
terms cancel provided one replaces
one finds that all
terms cancel provided one replaces
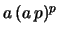 by
by
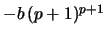 .
.
Note 5: The solution
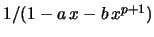 of this linear differential eq. with input
of this linear differential eq. with input
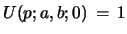 is unique. The proof is analogous to the one of proposition 5.
is unique. The proof is analogous to the one of proposition 5.
Note 6: If
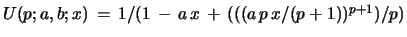 we do not have a formula for
we do not have a formula for
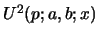 , valid for all
, valid for all 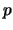 , like in the non-degenerate case. Therefore, we cannot derive results for convolutions
along the line shown above.
, like in the non-degenerate case. Therefore, we cannot derive results for convolutions
along the line shown above.
Lemma 11 (Recurrence in the degenerate case):
If
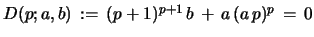 (and
(and 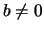 ) then one can replace the recurrence eq. 1 which
has depth
) then one can replace the recurrence eq. 1 which
has depth 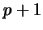 , by the following one with depth
, by the following one with depth
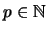 .
.
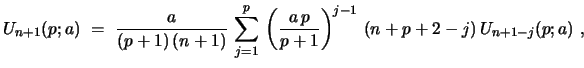 |
(73) |
where one uses the inputs
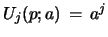 for
for
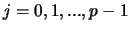 .
.
Proof:
This derives from the sum on the rhs of eq. 51 which now
vanishes. If the coefficients 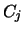 from eq. 52 are used with
the replacement of
from eq. 52 are used with
the replacement of
 by
by
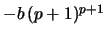 one arrives at the
desired recurrence, after the common factor
one arrives at the
desired recurrence, after the common factor 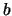 has been dropped. The inputs
are adopted from the original recurrence except that
has been dropped. The inputs
are adopted from the original recurrence except that 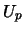 can now be
computed to be
can now be
computed to be 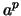 .
.



Next: Acknowledgements
Up: p35
Previous: Convolutions of generalized Fibonacci
Wolfdieter Lang
2002-04-04
![]() and
and ![]()
![]() is a polynomial in
is a polynomial in ![]() of
degree
of
degree ![]() , and
, and
![]() is one of degree
is one of degree ![]() . The sum in
. The sum in
![]() can be evaluated to yield the second of eqs. 47
provided
can be evaluated to yield the second of eqs. 47
provided ![]() .
.
![]() satisfies the first order linear differential eq. 57.
satisfies the first order linear differential eq. 57.