Research Group of Prof. Dr. Frans R. Klinkhamer
| Focus: fundamental aspects of elementary particle physics and structure of spacetime | ||||
Four main topics: | ||||
1. Baryon number violation through nonperturbative effects in the Electroweak Standard Model: | ||||
|
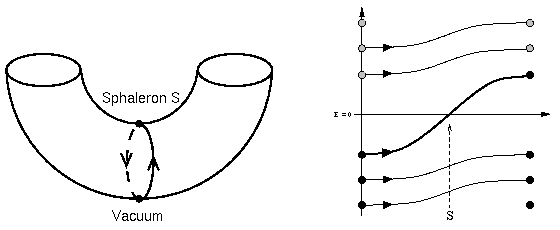
Sphalerons and spectral flow:
New results on spectral flow and sphalerons have been obtained in [Klinkhamer & Lee, 2001] and are under investigation. Two reviews: [Klinkhamer, 2002; Klinkhamer & Rupp, 2003]. The sphaleron $\text{S}$ is related to the Adler-Bell-Bardeen anomaly. Over the years, it has become clear that there are more sphalerons. In fact, there also exists a sphaleron $\text{S}^{*}$ related to the $SU(2)$ Witten anomaly; see [Klinkhamer, 1993]. And, finally, there exists a sphaleron $\widehat{\text{S}}$ related to the $SU(3)$ Bardeen anomaly; see [Klinkhamer & Rupp, 2005; Klinkhamer & Nagel, 2017]. | ||||
2. CPT anomaly: | ||||
|
Chiral gauge theories defined over a topologically nontrivial space manifold have an anomalous breaking of Lorentz and CPT invariance. An extensive review: [Klinkhamer, 2005]. | ||||
| ||||
| ||||
| ||||
| ||||
| ||||
3. Small-scale structure of spacetime: | ||||
|
The goal is to investigate a possible nontrivial structure of spacetime at very small length scales.
| ||||
4. Vacuum energy and cosmology: | ||||
|
Since 1998, it has become clear that there is not one cosmological constant problem but that there are three: | ||||
| ||||
|
Taking Lorentz-invariance seriously (cf. recent UHECR bounds on Lorentz violation in the photon sector [Klinkhamer et al., 2017]), a new approach [Klinkhamer & Volovik, 2008] to this set of problems is based on the following assumption: the perfect quantum vacuum can be considered to behave as a self-sustained Lorentz-invariant medium with a new type of conserved charge. The argument is based solely on thermodynamics (cf. Einstein 1907) and has an analog in condensed-matter physics (Larkin-Pikin effect, 1969).
Recent results are reviewed in
[Klinkhamer & Volovik, 2016;
Klinkhamer & Volovik, 2019].
| ||||
| Some talks: | ||||
|