Research Group of Prof. Dr. Frans R. Klinkhamer

Four main topics:

1. Baryon number violation through nonperturbative effects in the Electroweak Standard Model:

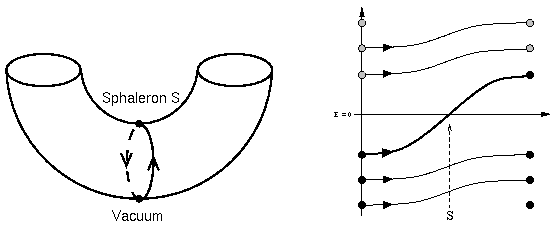
Sphalerons and spectral flow:

New results on spectral flow and sphalerons have been obtained in [Klinkhamer & Lee, 2001] and are under investigation.

Two reviews: [Klinkhamer, 2002; Klinkhamer & Rupp, 2003].

The sphaleron $\text{S}$ is related to the Adler-Bell-Bardeen anomaly. Over the years, it has become clear that there are more sphalerons. In fact, there also exists a sphaleron $\text{S}^{*}$ related to the $SU(2)$ Witten anomaly; see [Klinkhamer, 1993]. And, finally, there exists a sphaleron $\widehat{\text{S}}$ related to the $SU(3)$ Bardeen anomaly; see [Klinkhamer & Rupp, 2005; Klinkhamer & Nagel, 2017].

2. CPT anomaly:

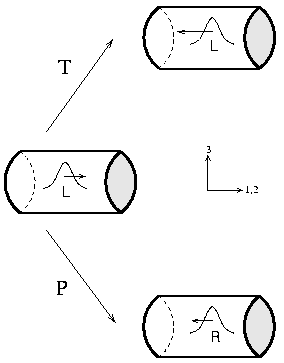
Chiral gauge theories defined over a topologically nontrivial space manifold have an anomalous breaking of Lorentz and CPT invariance. An extensive review: [Klinkhamer, 2005].

• Exact results in 2D and 4D [Klinkhamer & Nishimura, 2001; Klinkhamer & Mayer, 2001; Klinkhamer & Schimmel 2002].

• Modified Maxwell theory [Klinkhamer & Adam, 2001-02; Kaufhold & Klinkhamer, 2005; Kant & Klinkhamer, 2005]:
  • microcausality
  • photon decay (γ → 3 γ)
  • birefringence

• Microscopic structure of spacetime [Klinkhamer & Rupp, 2003; Klinkhamer & Rupp, 2005a; Klinkhamer & Rupp, 2005b]:
  • Spacetime foam affects photon propagation.
  • TeV photons from active galactic nuclei ⇒   l_foam < 1.6 × 10^-22 cm.

• Recent results are reviewed in [Klinkhamer, 2017].

3. Small-scale structure of spacetime:

The goal is to investigate a possible nontrivial structure of spacetime at very small length scales.

Two aspects have been considered in particular: The impact on the propagation of photons with wavelengths larger than the size of the "spacetime defects" (see, e.g., [Bernadotte & Klinkhamer, 2007; Klinkhamer & Schreck, 2008; Klinkhamer et al., 2017]). The detailed structure of one particular type of "spacetime defect" appearing as a soliton-type solution of the classical field equations (for a review, see [Klinkhamer, 2018]).

4. Vacuum energy and cosmology:

Since 1998, it has become clear that there is not one cosmological constant problem but that there are three:

• Why is |ρ_vac| << (E_Planck)⁴ ?
• Why is ρ_vac ≠ 0 ?
• Why is now ρ_vac ∼ ρ_matter ?

Taking Lorentz-invariance seriously (cf. recent UHECR bounds on Lorentz violation in the photon sector [Klinkhamer et al., 2017]), a new approach [Klinkhamer & Volovik, 2008] to this set of problems is based on the following assumption:

the perfect quantum vacuum can be considered to behave as a self-sustained Lorentz-invariant medium with a new type of conserved charge.

The argument is based solely on thermodynamics (cf. Einstein 1907) and has an analog in condensed-matter physics (Larkin-Pikin effect, 1969).

Recent results are reviewed in [Klinkhamer & Volovik, 2016; Klinkhamer & Volovik, 2019].

1. New type of traversable wormhole (Bahamas, February 2023)
2. Taming the Big Bang (Madrid, December 2022)
3. Cosmological constant problem: Revisiting the unimodular-gravity approach (Athens, October 2022)
4. IIB matrix model, bosonic master field, and emergent spacetime (Corfu, September 2021)
5. M-theory and the birth of the Universe (Cracow, January 2021)
6. Spacetime defects (Castiglioncello, September 2018)
7. On an anomalous origin of Lorentz and CPT violation (Faro, July 2017)
8. A new approach to the cosmological constant problem (Seoul, October 2015; Update January 2019)
9. Sphalerons and anomalies (an introduction) (Seoul, October 2015)
10. Elementary particle physics and cosmology for engineers (and others) (Karlsruhe, February 2013)
11. Superluminal neutrino: Theoretical considerations (Karlsruhe, December 2011)
12. Towards a derivation of G (Bremen, July 2010)
13. UHECR bounds on Lorentz violation in the photon sector (Penn State, August 2008)
14. Lorentz noninvariance and neutrino oscillations (Belgium, February/March 2006)
15. Nontrivial spacetime topology, CPT violation, and photons (Lisbon, July 2005)
16. Electroweak baryon number violation: basic mechanism (Ann Arbor, June 2003)